Important Note – These are descriptions to changes implemented in WoodWorks Shearwalls for version 9 and may not reflect current behavior.
Te equation implemented is the four-term equation from SDPWS Commentary Eqn. C4.3.2-1. It is
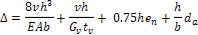
The meaning of the variables is given in the following sub-sections. The three-term equation given in SDPWS 4.3.2, Equation 4.3-1, is not used. According to SDPWS C4.3.2, the three term equation is a simplification of the four-term equation, one that does not take into account non-linear nail slippage effects, which have a significant impact on load distribution when stiffness is used to distribute loads.
The four terms in the equation give the contribution to deflection from the following sources, in order
For segmented shearwalls, the unit shear v is vertically accumulated strength-level shear force, that is, the shear force per unit foot unfactored by the 0.7 load combination factor for seismic design, as per ASCE 7 12.8-6. For wind design, it is the same as the force that is used for shearwall design and which appears in the elevation view at the bottom of the shearwall.
The unit shear used is the shearline force without the redundancy factor ρ applied. In some cases, ρ is 1.3 for shearline design, but it remains 1.0 for deflection analysis, according to ASCE7 12.3.4.1.
For perforated shearwalls, the v used is vmax, that is the force on the wall per unit distance of full-height-sheathing segment divided by the perforation factor Co , as per SDPWS 4.3.2.1. Co is given in SDPWS 4.3.3.5; vmax by Eqn. 4.3-9 in 4.3.6.4.1.1.
The second and third terms of this equation apply to the sheathing, which can be different for each side of a composite wall.. Both sides require a shear value v (the third term does so indirectly through en.). Refer to for an explanation of how shear is apportioned to each side of a composite wall.
The distribution of v within a shearline depends on the selection of Shearwall Rigidity per Unit Length and Distribute Forces to Wall Segments based on Rigidity in the Design Settings. For more details, refer to subsection 3 below
The shearwall height h is the distance from the bottom of the bottom wall plate to the top of the top wall plate, exclusive of floor joists or other building elements not part of the wall. This height is shown in SDPWS figures 4D and 4E for segmented and perforated walls, respectively.
For segmented shearwalls, the length b is the length of an individual full-height segment between openings, and the calculations are performed for each segment separately.
For perforated shearwalls, the length b is the sum of the lengths of the full-height segments, as per SDPWS 4.3.2.1, and one deflection is calculated for the entire wall.
The first term in the equation relates to the in-plane bending of the shearwall chords, that is, the wall end studs.
An input field has been added to Shearwalls to allow for input of the grade of the wood end studs. The modulus of elasticity is then taken from the WoodWorks database of material properties.
This is the section area end studs, which are typically built-up members. Shearwalls now allows you to input wall end stud thickness, width, and number of end studs (see ), from which the cross-sectional area is calculated.
Shearwalls does not allow for wall chord posts that are not made up of built-up wall studs but it is possible to model such a situation by typing in a value for the stud thickness, as it has no effect on shearwall design. However you cannot change the wall stud species to the one for the end post without having an effect on shearwall design, which depends on specific gravity. For MSR/MEL you cannot change the grade without having an effect on design.
The second term relates to the in-plane shear deformation of the shearwall
The value for shear stiffness Gvtv is taken from SDPWS Table C4.2.2A for wood structural panels and C4.2.2B for all other materials. The Sheathing Grades portion of the table is used, in accordance with Note 1 of the table.
In order to access table C4.2.2A, inputs have been added to Shearwalls for panel Span Rating, number of plies, and whether the panel is OSB. These inputs are described in subsection 4 below.
Refer to for an explanation of how shear is apportioned to each side of a composite wall.
The third term is related to the slippage of nails fastening the sheathing to the top and bottom shearwall chords, i.e top and bottom wall plates.
The fastener slip en is taken from SDPWS Table C4.2.2D. Note that the slip is non-linear with respect to shear-per-fastener Vn for wood structural panels, but does not depend on v at all for other materials ( it is a constant for gypsum, fiberboard, and lumber sheathing).
The load per fastener Vn is calculated by dividing the shear-per-unit-length v by the user-input panel edge spacing, yielding the force on each edge fastener.
The value v used to determine Vn is the strength-level v for seismic design ( see ).
Refer to for an explanation of how shear is apportioned to each side of a composite wall.
The 10d value is conservatively used for 16d nails, which may be selected for nail withdrawal strength for wind C&C loads.
The program does not limit the fastener shear to the maximum in Table C4.2.2D, or issue a failure warning in this case, as we determined that this level of loading always results in shearwall design failure for which a failure message is already output.
SDPWS Table C4.2.2D indicates that nail slip applies for lumber framing members with specific gravity of 0.5 or greater. As there is no guidance in SDPWS about what to do with materials such as S-P-F with specific gravity less than 0.5, analysis proceeds with the Table C4.2.2D values and a warning note appears under the Deflection table in the output.
For composite walls, the 2nd and 3rd terms of the equation, shear and nail slippage, apply separately to each side of the shearwall, which may have different materials. SDPWS 4.3.3.3.1 provides a way to apportion the total shear load on the segment to each side of the wall for the 3-term equation ( see ) but offers no guidance on the 4-term equation.
Shearwalls apportions shear to each side of the wall by adjusting the v value until the deflection due to shear plus nail slippage is the same on both sides of the wall. Note that this equalisation is done regardless of whether equalisation of deflections for all segments along a line is being done according to the selection of force distribution design settings described in subsection 3 below.
Slippage to non-wood-panel materials is a constant, which in many cases creates a larger slippage deflection than is possible for shear plus slippage even when all load is placed on the wood panel. In these cases, all the force is placed on the wood panel side. The deflection for that segment is the nail slippage plus shear from the wood panel side, not the constant
Note that in this case, despite the fact that all of the load is assigned to the wood side for purposes of deflection analysis and storey drift, the program still uses the sheathing on both sides of the shearwall for shearwall capacity calculations according to the procedures for combining shearwall capacity in the SDPWS.