|
|
|
|
|
Considering two adjacent levels with total story shear of FU above and FL below, the force to be distributed to shear lines on the lower level is F = FU + FL which is used to create the direct component of the lower level shear line forces Fdi . The torsional component of the forces Fti depends on the torsion T in the lower diaphragm, which is affected by the torsions and/or forces transmitted by the shear lines from the upper to the lower level.
A free body diagram of the upper level diaphragm is shown below. The forces on the upper diaphragm are
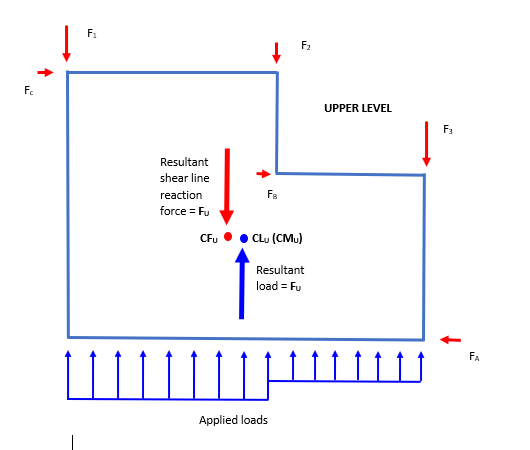
The effect of the shear line forces transferred to the lower level is shown below, where CRL is the center of rigidity on the lower level.
Adding the torsional moments shown, the component Tu coming from the upper level of the torsion TL on the lower level is
TU = Fu (CFU – CRL) + FU ( CLU - CFU) .
= Fu (CLU – CRL)
So the model can be simplified by using an effective force FU from the floor above situated at the center of loading of the upper level (center of mass in seismic design). Thus all the forces acting on the level below can be represented as shown below, in which it is assumed for clarity that there is heavier loading on the left hand side of the lower level than the upper (i.e. due to heavier seismic mass or greater area exposed to wind).
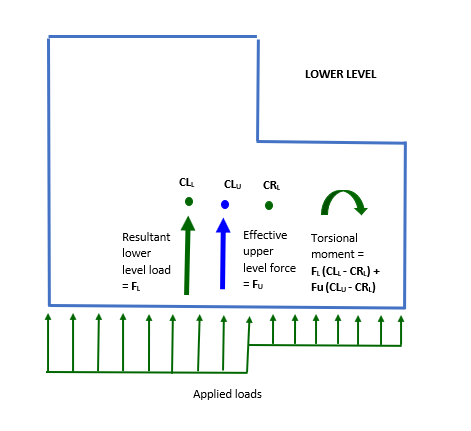
The torsional moment TL on the lower level is therefore
TL = Fu (CLU – CRL) + FL (CLL- - CRL)
This is sometimes expressed as
TL = F (CLL- - CRL) + Fu ( CLu - CLL),
i.e. the total load at the center of loading of the lower level, plus or minus the moment from the offset of the center of loads from of the upper level relative to the lower.
Refer to Transfer of Accidental Eccentricity for a continuation of this development that includes accidental eccentricity.