Derivation of Equation for Equal End Studs
The bending term in the deflection equation is derived by modeling the wall as a hollow cantilever beam with depth = wall length b and point load P = vb at end. The bending deflection of such a beam is
δb = Ph3 / 3EI
= vbh3 / 3EI
To calculate moment of inertia I, the parallel axis theorem is used, so that the moment of inertia of the two sets of end studs about their neutral axis is ΣIchord + Σ Ad2 ,
Ichord is the moment of inertia of the chords about their centroids and d is the distance from the neutral axis to the centroid of the chords. A is the cross-sectional area of the end studs.
The derivation ignores the contribution of Ichord and assumes the centroid of the wall stud is at the end of the wall. (as if the chords were infinitely thin, infinitely wide plates with area A.)
Under these assumptions,
I = 2 [ A (b /2 )2 ] = Ab2 / 2
Therefore,
δb = 2vh3 / 3EAb
Unequal End Studs
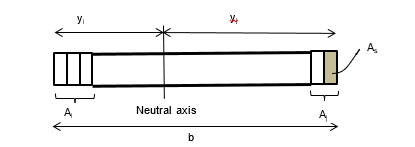
To calculate the moment of inertia I, let i and j be the number of studs at each end and As the area of one end stud.
Ii = Ai yi2 ; yi = j /( i + j) b , Ai = iAs
Ij = Aj yj2 ; yj = i / (i + j) b , Aj = jAs
I = Ii + Ij = ( ij2 + ji2 ) / (i + j)2 As b2
= i j / ( i + j ) As b2
Therefore
δb = 2vh3 / 3EAeffb
where
Aeff = 2 i j / ( i + j ) As
Effective End Stud Area
The following table gives the number of end stud areas As in the effective area Aeff for each combination of no of end studs i and j allowed in the program.
i or j |
1 |
2 |
3 |
4 |
5 |
1 |
1 |
1.33 |
1.50 |
1.60 |
1.67 |
2 |
|
2 |
2.40 |
2.67 |
2.86 |
3 |
|
|
3 |
3.43 |
3.75 |
4 |
|
|
|
4 |
4.44 |
5 |
|
|
|
|
5 |