If it were not for the constant component of hold-down displacement, the mathematical system used to model shear wall deflections would always arrive at a solution that equalized deflections along a line. This is shown below
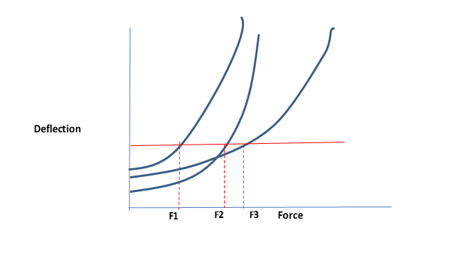
The red line represents the common deflection when deflections on all segments are equalized, and F1, F2, and F3 are the forces on the segments, which sum to the shear line force V. If we assume a curve entirely above the line receives zero force, as shown in Zero Forces on Segments , there is a solution for any force V = F1 + F2 + F3 due to continuity.
The only way non-linearity could cause a solution not to be achieved, or multiple solutions, is if there was a local maximum or minimum in the curves, as shown in the green curves in the diagram below.
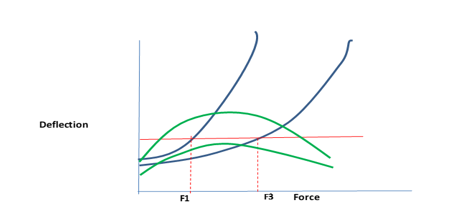
The deflection equation does not have a local extremum, implying that the equal deflection line drawn through them will hit all curves just once, and a unique solution will be found.
However, this guarantee of convergence depends on continuity, and discontinuities sometimes lead to non-convergence.