Dead Load Does Not Completely Counteract Overturning

Consider a dead load with magnitude q₁ at the tension end and q₂ at the compression end, which we distribute to the end chords over a distance l₁ at the tension end and l₂ at the compression end.

Using beam statics, the reaction to a partial load q over a distance l at the closest end is

  q  ( l  - l² /2L  )

At the far end of the segment, it is

 q (  l² /2L  ).  

The free-body diagram is thus shown below:

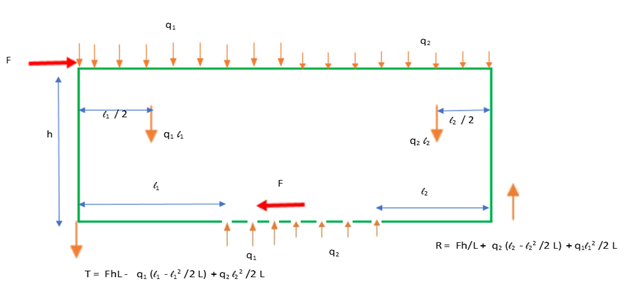
The arrows within the wall represent the centroids of the two sets of loads at top of the wall; the loads in between cancel with the reaction at the bottom.

To check that this is statically balanced, we sum moments about the left side:

M =  Fh + q₁ l₁ * l₁  / 2  +  q₂ l₂ ( L -  l₂  / 2 ) -  [ Fh / L  +  q₂ (l₂  - l₂² / 2L )  + q₁l₁² / 2L ] * L

    =   ( Fh  –  Fh ) + ( q₁ l₁² / 2 - q₁ l₁² / 2 ) + ( q₂ l₂² / 2 - q₂ l₂² / 2 ) + ( q₂ l₂ L -  q₂ l₂ L )

    = 0 .