Full Uniform Dead Load
Consider the case of a full uniform dead load q across the top of the wall, with shear force F, and define q' = 2Fh/L2 < q as the amount of dead load needed to completely counteract overturning. Assume the remaining load (q-q’) is passed straight through as the reaction at the base of the wall. Define O = Fh/L as the overturning force, where L is the shearwall length (for simplicity we will neglect the hold-down offset). The free body diagram is shown below:
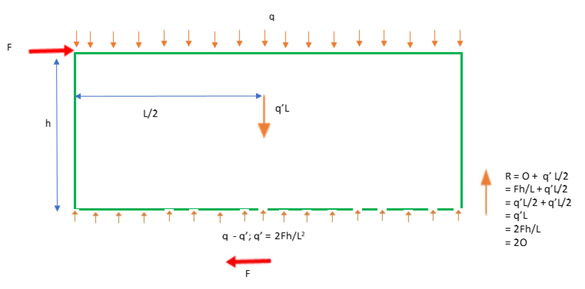
The arrow at the center represents the sum of the forces at the top and bottom, at the centroid of those forces.
To check static equilibrium, sum moments about the bottom left corner:
M = Fh + q'L* L/2 - q'L * L
= q'L2/2 + q'L2/2 - q’L2
= 0
About the bottom right:
M = Fh - q’L*L/2
= q’L2/2 – q’L2/2
= 0
Note that the compressive reaction at the end is twice the overturning force Fh/L, so the amount of dead load concentrated at that end equals the overturning force.
Partial Dead Load at Segment Ends
Consider the case that you have used the Dead or Wind Uplift Load Concentrated at End Chords setting to restrict the amount of dead load used to counteract overturning, but it still completely counteracts overturning.
Define
D’ = q1 (l1 - l12 /2L) + q2 l22 /2L
as the dead force at the tension end if all the dead load was used to counteract overturning. Refer to Dead Load Does Not Completely Counteract Overturning for definitions of these symbols and a derivation.
Define q1’ and q2’ such that q’ = q * O / D' , where O = Fh/L.
The free body of the wall segment is shown below:
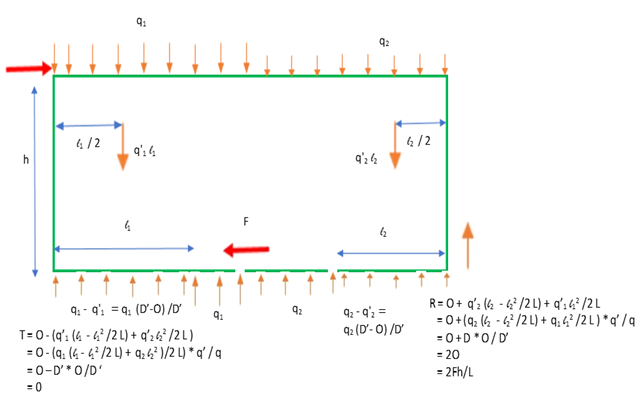
The force as the compression end is still twice the overturning force Fh/L.