Important Note – These are descriptions to changes implemented in WoodWorks Shearwalls for version 11 and may not reflect current program behavior.
The program now implements the story drift limitations from ASCE 7-10 Commentary Appendix C Serviceability Considerations, CC.1.2 Drift of Walls and Frames (page 580).
ASCE 7 CC.1.2 suggests limits in the range of 1/600 to 1/400 of the storey height. A design setting has been added to allow you to enter the drift limit to be imposed.
The storey height h used is the wall height plus the joist depth on the same level.
The wind speed to be used is from the maps in Figures CC1 to CC4 of ASCE 7-10, corresponding to mean recurrence intervals (MRI) of 10, 25, 50, and 100 years, respectively. It is up to the designer’s judgement as to which of these to choose.
A new data group has been added to the Site Dialog called Wind speed, which includes the input MRI (serviceability) to allow you to enter the value for your area from these maps. The existing input for shearwall design has been renamed Basic (MWFRS).
The default for new files is 100 mph.
Unlike the design wind speed, the program does not currently allow you to save a value as default for new files; it must be reset for every project.
The load combination employed is D + 0.5L + Wa, from ASCE 7 CC.1.2.
This combination is used for serviceability calculations only, i.e., for the in-plane shearwall deflection to be compared to drift limits. It is not used for the deflections used to distribute loads for shearwall design; these now use the ASD load combination from 2.4.1, 0.6W + 0.6D. (Previously strength-level load combination was used, see item for a description of that change).
The wind load Wa is derived from the serviceability wind speeds using the same provisions that are used to generate wind loads for shearwall design from ASCE 7 Chapters 26-28. The only difference is the wind velocity used to create pressures in 27.3.2 and 28.3.2.
In determining deflections, Wa is used for:
The dead load factor is 1.0, as opposed to the 0.6 ASD factor for MWFRS deflections used for force distribution for shearwall design. These factors are for dead loads counteracting the wind overturning hold-down force
The 0.5L component is considered, as the program does not include live loads. In any event, it is not clear that these loads are permitted as counteracting loads or are intended only to increase deflections, as one cannot depend on the occupancy load to be present.
The program does not create a separate load case to determine shearline forces for drift-limit deflection; instead, it uses the ASD shearline forces multiplied by a factor α representing the difference in wind pressures between those used for serviceability and for MWFRS design, as well as the difference in load combination factors. Since wind pressures are given in ASCE 7 27.3.2 and 28.3.2 by P = d * Kz * Kd * Kzt * V2 * G * Cp, in which all terms except for V are the same, this factor is
α = PSERV / PMWFRS / 0.6 = (VSERV / VMWFRS)2 / 0.6
The assumption that shearline forces are proportional to wind pressures is not strictly true for the rigid diaphragm method due to nonlinearity in the torsional distribution to shearlines. However, for typical asymmetric buildings with a significant torsional component, the difference in shearline forces using this approximation compared with generating and distributing reduced wind loads Wa is less than 1%.
The program makes a separate set of defection calculations for ASD design of shearwalls, to distribute shearline forces to the shear resisting elements. Unlike serviceability deflections, the wind speeds used to generate the force for these deflections depend on Risk category; however, they do not depend on a discretionary selection of recurrence interval (MRI).
Using the southern tip of Florida as an example, the factored forces resulting from serviceability wind speeds and load combination range from 34% of the ASD forces for Risk Category III/IV buildings at 10-year MRI to 130% of ASD forces for Risk Category I at 100 year MRI. For a typical case of Risk Level II (Normal) at 50-year MRI, serviceability forces are 87% of ASD forces.
The process of distributing forces to segments in a line such that they equalize deflections is performed independently for serviceability wind forces. Because some of the deflection components are constant with respect to v, one cannot rely on the distribution of forces achieved with the MWFRS wind speed and just factor each segment force by α, as we do with shearline forces. If capacity-based distribution to segments is used, it is possible to do so.
As the program now gives you the option of using the 3-term deflection equation from SDPWS 4.3-1 (see item ), a question arises as to what apparent shear stiffness Ga to use for serviceability wind loads. The SDPWS publishes Ga values for seismic design only, and does not offer guidance on wind loads.
We have implemented a procedure for serviceability wind loads that is analogous to the procedure for seismic loads using the SDPWS Equation C4.2.3-3. Instead of using 1.4 vs,, we use α vw where α is defined in the previous subsection. This procedure applies to wood structural panels only; for other materials, we use unfactored vw, which results in a Ga close to what is published in the SDPWS for seismic design.
Although this procedure was developed by WoodWorks it has been approved by AWC.
The Ga value is calculated for seismic design using is a linear approximation of the 4-term equation arrived at by combining the multiplicands of v in the 3rd and 4th terms into an "apparent" shear stiffness.
The linearization is achieved by setting all non-linear instances of the shear force v in Ga to the value at shearwall capacity, vs. This means that the 3-term and 4-term equations are the same at full shearwall capacity, and ensures that the linear 3-term deflections are conservative with respect to the non-linear 4 term ones for all shearwalls that have sufficient capacity to resist the applied shear force. Refer to SDPWS figure C4.3.2 for a graph of this linearization process.
For seismic design an adjustment is necessary, because deflections are calculated using v’s for Strength-level design, with a load combination factor of 1.0, however the shearwall capacity vs is for ASD design, which has a factor of 0.7. Therefore, to ensure that the 3-term approximation is conservative for all shearwalls that pass ASD design, the value 1.4 vs is used. (For historical reasons, SDPWS rounds the factor to 1.4 rather than using 1 / 0.7, which converts ASD forces to strength-level forces).
For serviceability wind loads, the v’s used for deflection calculations are the ASD design forces multiplied by α, which includes the serviceability wind speeds and the serviceability load combination factor. Therefore, the serviceability v at the point at which the shearwall is fully loaded is α vw.
Some users may not be comfortable with using Ga values other than those published in the SDPWS for seismic design, especially since they are the same Ga values used, by coincidence, for MWFRS wind design with wood structural panels. Although Ga is published in SDPWS as a physical parameter, it is not a physical property of the sheathing in the same sense as Gvt, which is used in the 4-term equation; it is also an artifact of the linearization procedure used to convert 4-term to 3 term, in that it is highly dependent on the point chosen to intersect the 3-term and 4 term equation.
If the published Ga were to be used, in most cases it would cause the 3-term to intersect the 4-term at a point far above the point at which shearwalls are fully loaded. As an example, for a shearwall that is 80% loaded, for 10 year MRI this causes shear/slip deflections for the 3-term equation to be 2-3 times higher than they would be using the α factor. For a typical case of 50 year MRI, Normal risk level, the deflections are 28% higher. This would be problematic as designers often have difficulty meeting stringent drift limitations.
For 100 year MRI, the equations intersect below the point that the shearwall is fully loaded, so that the 3-term deflections would be non-conservative with respect to 4-term by as much as 40%.
For fiberboard and gypsum wallboard, the nail slippage in the 4-term equation is constant, and the 4-term equation is not in fact non-linear. The effect of Ga the 3-term equation is to vary the shear component deflection from 0 to the deflection at shearwall capacity, rather starting at the constant shear nail slip value. The arguments in the previous sections therefore do not apply, and we were instructed by AWC to use the published Ga values for seismic design for these materials.
When calculating hold-down displacements, the strength-level values from the hold-down database are used, as the wind load combination factor 1.0 is the same as it is for strength-level design. Note that ASD values are now used for MWFRS deflections.
Refer to section G6r)ii for changes to the Design Results output arising from this feature.
Because serviceability shearline forces were derived from ASD forces, as described above, serviceability wind loads were not generated and do not appear in the log file. Torsional analysis for serviceability wind loads is not performed independently and does not appear either.
Because serviceability shearline forces were derived from ASD forces, as described above, serviceability wind loads were not generated and do not appear in the Plan view when Generate Loads or Loads and Forces is selected. Neither is there an option at present to show the forces derived from serviceability wind loads in Loads and Forces view.
Shearwalls now offers the choice of using the linear 3-term deflection equation from SDPWS 4.2-1 and the non-linear 4-term equation from C4.3.2-1. Previously only the 4-term equation was implemented.
The 3-term equation is a linearization of the 4-term equation, arrived at by combining the shear and nail slip equations in the 4-term equation using an "apparent" shear stiffness Ga. The linearization is achieved by setting the non-linear occurrences of shear force v to the shear capacity of the shearwall to render them constant. It is therefore identical to the 4-term equation when the shearwall is at capacity, conservative when below capacity, and non-conservative for shearwalls that are overstressed for design anyway. SDPWS Figure C4.3.2 shows this in graphical form.
The four-term equation was originally implemented in Shearwalls because it is more accurate and because the SDPWS does not publish Ga values for wind design. However, the process of equalizing deflections on the shearwall segments by adjusting the forces apportioned to each segment sometimes does not converge due to the non-linearity of the 4-term equation, whereas the 3-term equation always converges to a solution. Also, some users are more comfortable using the 3-term equation because it is in the main body of the SDPWS, whereas the 4-term equation is in the Commentary.
A Design Setting has been added to allow you to choose between these two methods. It is recommended to use the 4-term equation, but switch to the 3-term if using the deflection-based force distribution method and one or more of the shearlines do not show the same deflections on each loaded shearwall segment in the line.
Note that SDPWS commentary C4.3.2 cautions against mixing the two methods in the same design, as it can adversely influence force distribution based on relative stiffness. This is true within a line, and possibly distribution to shearlines if the rigid distribution method is used. For a future version we will consider allowing the program to automatically change from 4-term to 3-term on individual shearlines if non-convergence is detected, especially using flexible distribution; however, for Version 11, the switch must be made manually and for all shearlines in the structure.
The SDPWS lists Ga values for seismic design only, and gives design examples using the 3-term equation and showing how to calculate Ga for only for seismic design. However, Shearwalls allows this method for wind design, with the adjustments to the calculation procedure given below.
The following terms in the two-term equation
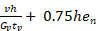
are replaced by
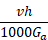
The calculation of Ga for seismic design uses the formula
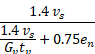
The factor 1.4 ≈ 1/0.7 ensures that the v is evaluated at the maximum allowable shear for ASD design, given that the v value in the deflection equation is calculated using strength design. (1.4 is used rather than 1/ 0.7 for historical reasons.)
is evaluated at the maximum allowable shear for ASD design, given that the v value in the deflection equation is calculated using strength design. (1.4 is used rather than 1/ 0.7 for historical reasons.)
In most cases, the value of Ga is the same as that listed in Table 4.2B, but it may be slightly different because the use of the equation allows us to consider the number of plywood plies when evaluating Gvtv., whereas note 3 of Table 4.2B approximates this effect by applying a factor of 1.2.
For wind deflections for MWFRS force distribution, the same expression is used without the 1.4 factor, because we now evaluate deflections with ASD forces and there is no need to convert from ASD design to Strength deflections.
For wood structural panels and fiberboard, this results in the same Ga values as for seismic design because the shearwall capacity vw = 1.4 vs. It is important to note that this is merely a coincidence; the difference in capacity for wind vs. seismic is for unrelated reasons pertaining to a historical increase in design wind loads related to test strengths. The increase was not applied to other materials such as gypsum wallboard, and these have different Ga values for wind vs. seismic design.
Shearwalls 11 includes a new set of serviceability deflections for story drift determination, described in the preceding section, which also includes the calculation of Ga for serviceability wind forces.
The unblocked factor Cub is applied only to the v value in the main deflection equation. not the vs and vw values in the calculation of Ga. This is consistent with SDPWS Eqn. C4.3.2.2-2, where it is shown that dividing v by Cub is equivalent to factoring the whole shear stiffness Ga by Cub.
As per Commentary C4.3.2.2, the capacity Increase for 3/8" and 7/16" sheathing under certain framing conditions from Table 4.2A Note 2, is not applied to vs or vw for unblocked shearwalls for the purpose calculating Ga.
Refer to for changes to the Deflection table arising from this feature.
On the advice of AWC, Shearwalls now calculates deflections to distribute forces to the main wind force resisting system for shearwall design based on the ASD load combination 0.6D + 0.6W from ASCE 7-10 2.4. Previously Strength-level deflections were used, using 0.9D + 1.0W, from ASCE 7-10 2.3, because they are required for seismic design by 12.8.6 and the ASCE 7 does not offer guidance on wind design.
The wind load factor changes from 1.0 to 0.6 for the shearline force v, for wind uplift hold-down force, and for the effect of hold-down forces from upper levels.
The dead load factor changes from 0.9 to 0.6 for the counteracting dead load component of hold-down force.
Previously the hold-down database had only strength-level deflections. It has been expanded to include ASD deflections to be used for ASD wind design. Strength-level deflections are retained for seismic design and for serviceability wind loads for story drift calculations.
To implement the new SDPWS provision 4.3.2.3, if there is fiberboard on either side of a wall segment with an aspect ratio greater than 1:1, the total deflection for the segment is multiplied by (h/b) ½.
If there is any fiberboard in the structure, the application of this factor is mentioned in the Legend to the Deflection table, however the actual value of the factor is not listed in the table.
If you specify via the Design Settings that shearwall capacity is to be used as the design force for hold-down design, this value was also used to determine the hold-down component of shearwall deflection. As this is not the intent of the use of shearwall capacity to ensure sufficient hold-down strength, the calculation for deflection now always uses applied force to determine hold-down displacement, regardless of the design setting for hold-down forces.
Occasionally, warnings appeared indicating the program had not equalized deflections on the shearline, when the Design Results output showed identical deflections along the line. This was because the tolerance for equalizing deflections internally was 0.01% of the deflection value, which is unnecessarily stringent. It has been changed to .5%", which ensures that when deflections are not equalized to that level, it is apparent in the output table.
Occasionally, for two-sided shearwalls, the program would show v, vmax, and Critical response values in the Shear results table as dashes or blanks, even though there is a total force V on the wall in question.
This was due to an intermittent failure in the process equalizing deflections on either side of the wall, and has been corrected.