|
|
|
|
|
Allowable Stress Fv' vs Design Shear Vr'
The shear design equation at supports without notches was given in the NDS 2018 in terms of the allowable shear stress Fv' and actual shear stress fv whereas in Sizer 20124 the "design shear" Vr' and actual shear force V are used. A similar change occurred for notched supports for the 2001 edition of the NDS, previously Fv' and fv were used with a notch factor Cn but since 2001 the design for notches use formulas based on Vr and V without the notch factor. Note that the force formulation is just an algebraic reorganization of the one using stress and does not represent a substantive change to the design procedure.
In order to have a consistent format in our design reports, Sizer continued to use the formulation using Fv' and fv for both notched and unnotched members, and we derived the notch adjustments to Fv' that were equivalent to the reduction to Vr, given in the NDS . We show the formulation in the CALCULATIONS section of the Design Results.
Given that both notched and unnotched members now use the formulation using V and Vr', an upcoming release of Sizer will change the design methodology accordingly. The following gives the organization of the provisions in NDS 2018 3.4; it will be updated when the program methodology is changed.
3.4.2 Actual Shear Stress
The calculation of actual shear stress fv for sawn lumber, glulam and SCL members is given in NDS 2018 3.4.2, where
fv = 3V / 2bd,
where V is the shear force at the member section.
The factored shear stress is fv compared with the factored allowable shear stress Fv'.
An upcoming release of Sizer will show the equation in terms of design shear Vr and shear force V as it is in the 2024 NDS; however the formulation used in Sizer gives the same design results as the one in NDS 2024, as the equations are algebraically equivalent.
Refer to NDS 7 - Wood I-Joists for I-Joist shear design and for PRG 320 Table A-2 and O86 8.4.4.2 - Shear Resistance for CLT shear design.
3.4.3-Shear Design
3.4.3.1 Shear near support
Sizer applies the provisions of NDS 3.4.3.1 by adjusting the shear values calculated using the actual loading conditions of the member. For each load combination, the shear value at the support is reduced by the portions of the shear resulting from each load within the distance “d” of the edge of the support.
In other words, Sizer takes literally the provision that loads within a distance d of a support "shall be permitted to be ignored" . This is slightly different than taking the value of the shear a distance d from the support, as the latter approach does not take into account the contribution to the reaction at the other end of the member of the ignored loads.
Because the adjustments are done after the loading analysis, the contribution of each load to be ignored is distributed proportionally only in the two supports enclosing the current span. This provides exact values of the design shear for single span members and exact or slightly conservative values for multi-span members.
Sizer measures the distance d from the inner edge of the support, as per NDS Figure 3C. Sizer performs iterative design , first determining required bearing lengths assuming d is measured from the support point, then using these to establish the point from which to measure d on the next iteration.
Uniform and non-uniform distributed continuous loads are ignored within distance "d". Point loads are factored as per NDS 3.4.3.1.a. Uplift continuous loads are not ignored, and uplift point loads are not factored.
For a particular load combination, the shear near support is reduced only if there is not an uplift reaction at that support.
Point loads applied on top of sloped members have the position along the member bottom calculated according to the load type (see loads on sloped members) and the member’s depth. This position is then and used in conjunction with the distance “d” point load for the factoring of the magnitude
3.4.3.3-Shear Design for Bending Members at Connections
The effect of connections on the shear capacity of bending members has not been implemented in WoodWorks Sizer. It is planned for the next update of the program.
3.4.3.2 - Shear Design for Notched Bending Members
Tension or compression face determination
You input the value of the unsupported length “e” and Sizer aasigns this value to the compression face notches.
If a design has not been performed, the program will consider the top of the member to be the compression edge and assign the “e” to the top notches. When a design is performed, Sizer determines if a notch is on the tension edge or the compression edge by checking the bending orientation at the interior end of the notch. For this purpose, Sizer automatically creates points of interest at these locations.
Length restrictions
While all tension face notches are assumed to be the support length, the compression face notches will be the support length plus the unsupported length “e”.
If the “e” value causes any compression face notch to be more that 1/3 the length of the associated span, which is disallowed by NDS 4.4 and 5.4- Special Design Considerations, the the program warns you upon designing the beam. It will then simply reset the unsupported notch length “e” to 1/3 the span length and proceed. The notch length will be adjusted for both (if existing) compression face notches.
Sloped members
Sizer assumes that the notch depth entered by the user is always perpendicular to the member, and that the unsupported length “e” is along the horizontal projection of the member.
Notch diagrams
Notches are not shown in the beam diagrams if the member has not yet been designed or if it is a sloped member. Instead, a note below the location mentions the existence of the notch.
Notch Adjustment to Allowable Shear
The shear strength reduction for allowable shear is given in the NDS in terms of the "design shear" Vr', however shear design for unnotched members is presented in both the NDS and Sizer in terms of allowable and actual stresses Fv' and fv. We have derived the adjustment to Fv' that is equivalent to the reduction to Vr, and give both the equation and value in the CALCULATIONS section of the Design Results output for each case of tension and compression edge notches. Below this adjustment is called Cn based on terminology that was once in the NDS; this this factor no longer appears as such in the NDS
Shear Strength Reduction - Tension edge notches
NDS equation 3.4-3 gives the shear reduction due to tension edge notches:
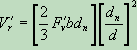( NDS Equation 3.4-3)
Where dn is the depth remaining after a notch is taken out. Given the usual equation for shear, this establishes the following value for the notch adjustment, given as Cn as it appeared in pre-2021 versions of the NDS.
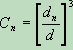
In NDS 1997, this equation was formulated by factoring Fv rather than Vr, however the equivalent notch factor was the reciprocal of this ratio raised to a power of 2 rather than 3.
Shear Strength Reduction - Compression edge notches
NDS equation 3.4-5 gives the shear reduction due to compression edge notches:
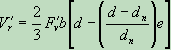, for e <= dn (NDS Equation 3.4-5)
Shear reduction for compression edge notches , e > dn:
, for e > dn.
Given the usual equation for shear, this establishes the following value for the notch adjustment, given as Cn
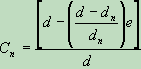, for e <= dn
or
, for e > dn
Biaxial Shear Design
The NDS gives no guidance on how to deal with bending shear for members loaded on both faces. In Sizer, this currently applies only to beams with an oblique rotation angle. Refer to Oblique Loading for Sizer's design methodology for beams rotated with respect to the load.